Het idee achter de bootstrap is om een schatting te maken van de onzekerheid in de berekende kalibratie waarde.
Wat theoretische details staan op:https://en.wikipedia.org/wiki/Bootstrapping_(statistics)
We onderzoeken twee parameters in het bootstrap algorithme door in de voorbeeldcode een parameter tegelijk
te varieren
- nrboots
- teruglegfractie
We nemen onze huissensor LTD_22268 en de vaste dag 1 April 2021, omdat op die dag, zowel voor
RIVM stations als oor citizen science een grote PM2.5 berg te zien was.
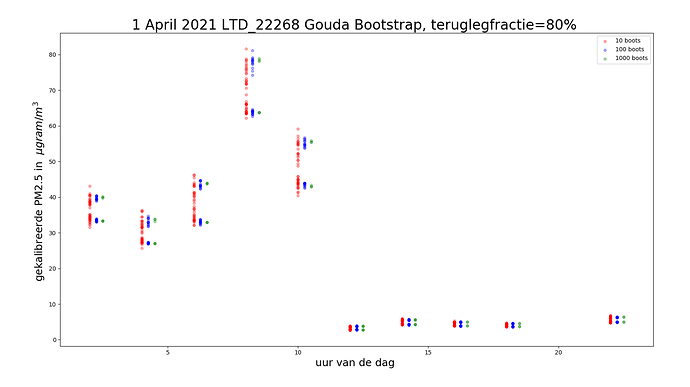
We zien in onderstaand plaatje dat het aantal keren teruglegging tussen 10 en 100 de onzekerheidsmarge vermindert. Tussen 100 en 1000 scheelt het resultaat nauwelijks.
We kunnen dus met 100 boots volstaan, dat scheelt weer computercycles !
at verder opvalt is dat de gekalibreerde waarde zelf niet symmetrisch tussen de minmale en maximale
schatting zit, zie onderstaande tabel.
Het waarom hiervan hopen we in een volgend theoretisch bootstrap stuk zelf te begrijpen en vervolgens ook te kunnen uitleggen.
nrboots datumtijd terugleg station X Y ruw kal kalmin kalmax
100 2021040102 20 LTD_22268 108973.0 446993 23.07 35.512554 31.308540 45.298584
100 2021040104 20 LTD_22268 108831.0 447032 19.44 28.717118 25.864363 34.452968
100 2021040106 20 LTD_22268 108886.0 447088 23.09 36.711646 30.779156 62.825227
100 2021040108 20 LTD_22268 108904.0 447139 54.96 67.682307 61.131577 80.249577
100 2021040110 20 LTD_22268 108901.0 447033 29.70 46.838210 36.645935 72.356005
Het volgende experiment is om te draaien aan de teruglegfractie.
In de voorbeeldsourcecode staat de teruglegfractie standaard op 80%.
Wat het voordeel is boven standaard 100% teruggeleggen, is mij nog niet duidelijk.
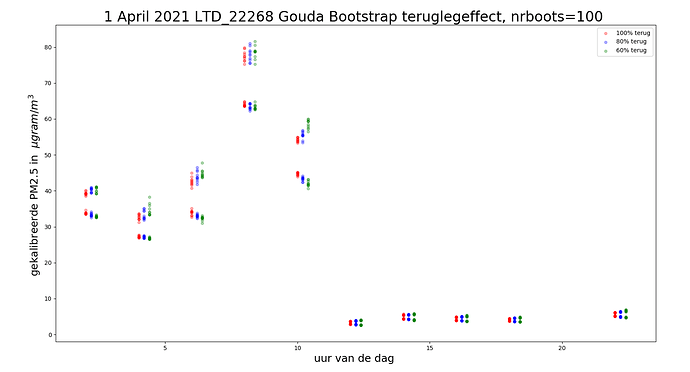
In onderstaand plaatje zie je dat door 80% terugleggen een grotere statistische onzekerheid wordt
verkregen, dan bij 100%.
In de ene bootstrap cyclus neem je de ene set mee, in de andere een andere, dus dat je bij minder terugleggen een grotere onzekerheid krijgt, lijkt intuitief ok.
De onzekerheid bij de hoge waardes is intrinsiek groter dan bij lagere waardes, daar verandert de teruglegfactor niets aan.
Betekent de terugleg parameter alleen statistisch iets of ook fysisch ?
Zou je je niet willen beperken tot de meest nabijgelegen rivmstations, of ga je ervan uit door de omgekeerde afstands afhankelijkheid (zie KAFE_02) dat verder gelegen toch weinig meedoet.