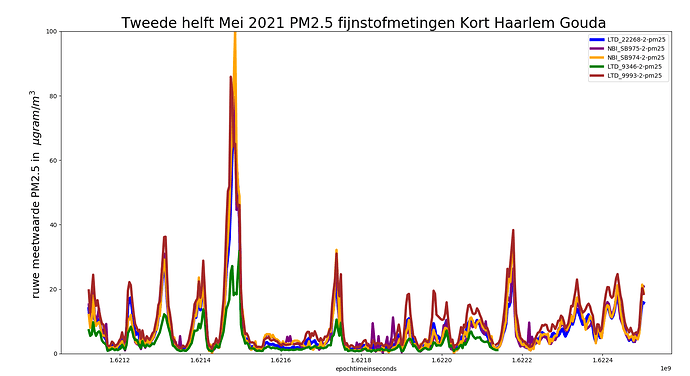
We nemen een nabijgelegen set van 4ster plausibele sensoren in het Goudse, binnen een paar 100m
vanaf mijn thuislocatie, in de Goudse wijk die verwarrenderwijs Kort Haarlem heet.
Het waarom daarvan heeft niets met fijnstof te maken, zie Mysterie opgelost: dit is waarom deze wijk Kort Haarlem heet - indebuurt Gouda
Het huidige rivm algoritme neemt elke sensor als een onafhankelijke meting en kijkt alleen naar
het statistische gemiddelde van grote groepen.
Een gelijkvormige nabijgelegen groep is statistisch krachtiger dan losse sensoren. Als de hele goep hetzelfde patroon volgt, en dat patroon wijkt af van een nabijgelegen rivm station,
dan is er een indicatie voor een locale oorzaak.
Als die lokale oorzaak luchtvochtigheid is, dan zijn we snel klaar en beschouwen het als artefact.
Als de lokale luchtvochtigheid laag is, dan is er misschien iets anders aan de hand…
Op 1 April was de luchtvochtigheid niet extreem (zie https://www.meteo-gouda.nl/ )
We zien verschillende hoge uitslagen van nabijgelegen SDS011 sensoren.
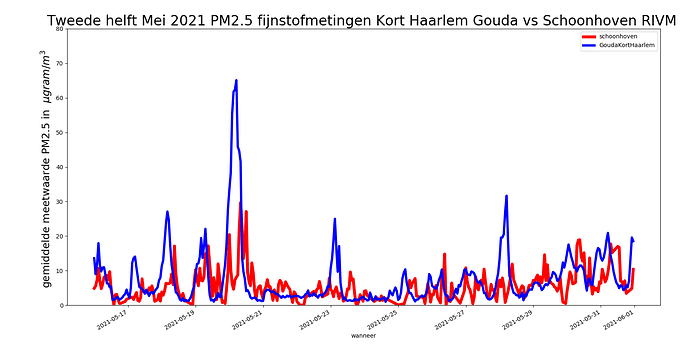
Het RIVM station Schoonhoven heeft maar een zeer bescheiden piekje, vergeleken met het gemiddelde van onze set Goudse sensoren ;zijn we iets op het spoor ?
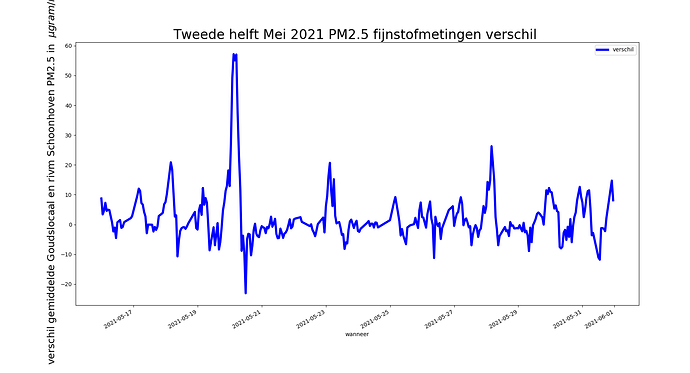
We plotten het verschil tussen het gemiddelde van de Goudse sensoren en het RIVM station Schoonhoven:
We plotten het verschil tussen het gemiddelde van de Goudse sensoren en het RIVM station Schoonhoven:
Dat lijkt wel een effect ?
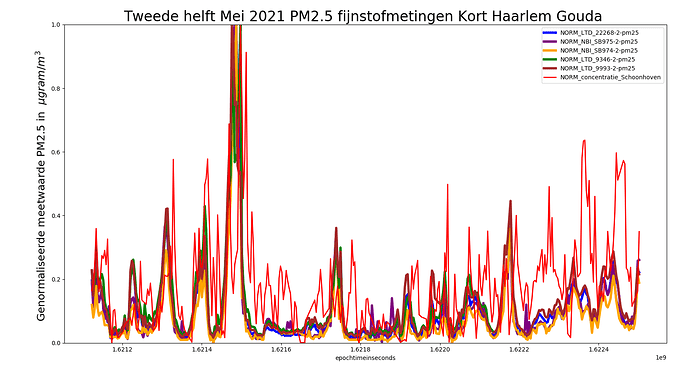
Maar kijken er weer weer op een andere manier tegenaan door de maximale uitslag te normeren de op 1, dan krijgen we onderstaand plaatje
Met ook RIVM station Schoonhoven genormaliseerd toegevoegd in de rode kleur.
Dan lijkt het RIVM patroon toch weer verdacht veel op het locale Goudse patroon:
Wat hebben we geleerd voor de volgende keer ?
1)korte extreme pieken vertekenen het gemiddelde nogal,
Simpele outlier schemas werken niet als bv:
gooi de hoogste en de laagste uit de groep weg,
gooi alles weg boven max waarde
2)normaliseren op 1 is een techniek om nog eens vaker te proberen.
Nieuwe rondes, nieuwe kansen !