In de recente rivm publicatie “Assessment of PM2.5 Exposure during Cycle Trips in The Netherlands Using Low-Cost Sensors”, waarnaar in dit forum al verwezen werd ( Rapport over fijnstof happen tussen het autoverkeer ) , komt een variant om de hoek van het algoritme dat wij bekijken.
De data van dit onderzoek zijn downloadbaar (GIS | Samen meten aan luchtkwaliteit ), wat weer een zee aan nieuwe mogelijkheden voor zelf experimenteren opent.
MySense heeft nu over enkele jaren een schat van metingen in een data base verzameld (ca 100GB). Walter als je wat data nodig hebt email me.
Samen Meten: we modderen maar wat aan
Het is al eens eerder geopperd. Een soort standaard tav uitwisselingsformaat (het gaat met name om welke data “noodzakelijk en voldoende” is met een flexibiliteit voor uitbreiding is mi noodzakelijk. Een voorstel hiertoe heeft weinig respons (zie enkele presentaties) gehad. Een jaar geleden strandde een voorstel om een soort centrale publiekelijk en vrij (lees: freedom) beschikbare meetdata database in Nederland (lees: .nl) in te richten. Eerste verkenning was een kleine investering: ca 100.000 euro is benodigd voor 5 jaar. Iets voor een ministerie (I&W?) om dit te innoveren? Kan ieder zijn/haar dashboard van data voorzien…
Ik zal niet nalaten dit nogmaals te benoemen in een presentatie over Samen Meten en citizen science (lees: burgerkunde).
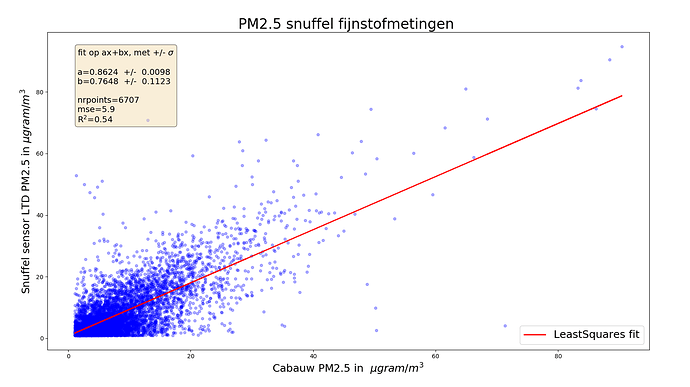
We analyseren figuur 5d (Snuffelfiets PM2.5 vs RIVM Cabauw) van het al eerder aangehaalde snuffelfiets artikel.
Tot ons genoegen kunnen we het plaatje zelf reproduceren (met de ter beschikking gestelde openbare data) en vinden dezelfde correlatiewaarde als in het artikel staat:
Een bekende facor die meetwaardes beinvloedt is de relatieve luchtvochtigheid.
De onderzoekers hebben er expliciet voor gekozen om deze niet mee te nemen
Helaas kunnen wij die niet zelf toevoegen omdat er in de beschikbare data geen datumtijd beschikbaar is.
Wat wel opvalt is dat de lage meetwaardes veel vaker voorkomen dan de hogere.
Op zich niet zo verwonderlijk, want het fijnstofgehalte is vaker laag dan hoog.
De correlatie waarde met Pearson is 0.73, wat op zich niet heel hoog is.
Gebruiken we andere methodes (Spearman, Kendall) dan valt de correlatiegraad lager uit.
Dat de meetwaardes niet zo uniform verdeeld zijn, brengt toch wat ongemakkelijke jeuk teweeg,
daarom gaan we rigoreus aan de slag:
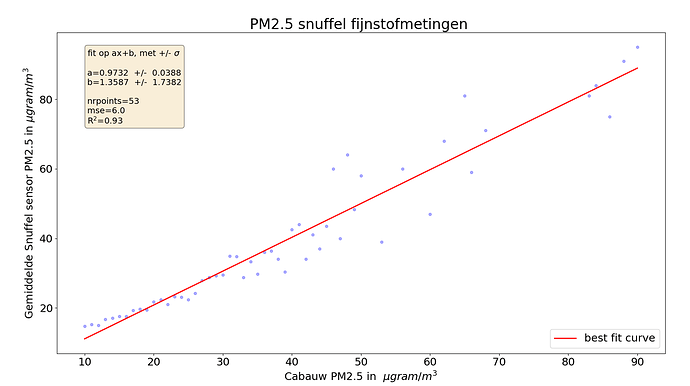
1) we gooien alle waardes onder de 10 ugram/m3 weg
2) we ronden alle overblijvende Cabauw waardes af op gehele getallen
3) bij elk Cabauw getal nemen we het gemiddelde van de snuffelfiets waardes in die "kolom"
Met ons vertrouwen op de wet van de grote getallen, komt er een mooi correlerend plaatje uit:
De gemiddelde fout neemt niet heel erg sterk af, wat maar weer aangeeft dat mean squared error vaak een betere maat is dan (Pearson) correlatie.
Een interessante aanname is dat er in dit paper een eis gesteld wordt aan de spreiding van
fijnstofwaardes over de utrechtse stations voordat kalibratie toegepast wordt.
De standaarddeviatie mag maximaal 15% zijn van het gemiddelde van de Utrechtse stations.
Geen onterechte eis, omdat het hier een sterk locaal experiment betreft.
Maar het stelt wel de interessante vervolgvraag hoe vaak dit gebeurt of wat of de oorzaak
zou kunnen zijn van het uiteenlopen van meetwaardes naastgelegen RIVM stations.
Dit alles verandert niets aan de conclusie van de paper dat “de bijdrage van verkeer aan PM2.5 fijnstofgehalt, is orde 2 ug/m3 is” en dat er wel degelijk goede en foute routes bestaan, (zie Figuur13 en 14, waarbij ik vind dat de kleurcodering wel een zeer niet lineaire indeling kent met rood van 2.7 tm 72 ug/m3)
