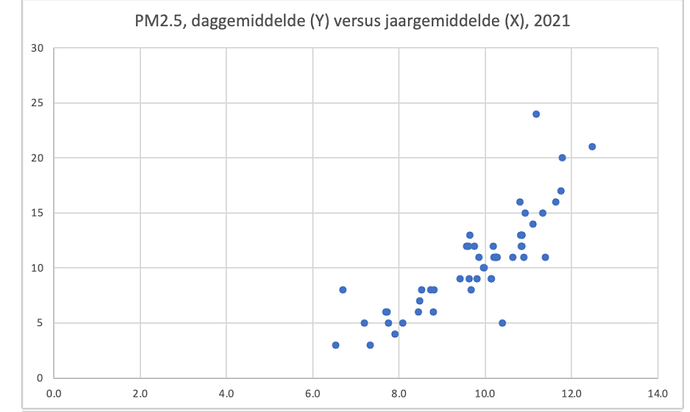
De vraag die ter beantwoording ligt is die van - wat is de kans dat er een x aantal dagoverschrijdingen van y mmgr/m3 plaats vindt gegeven een jaargemiddelde van M0?
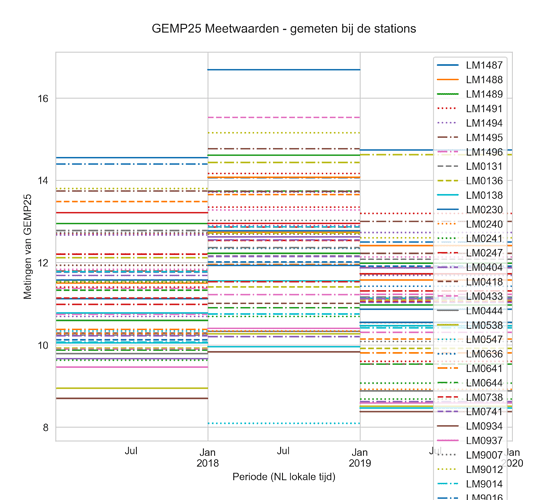
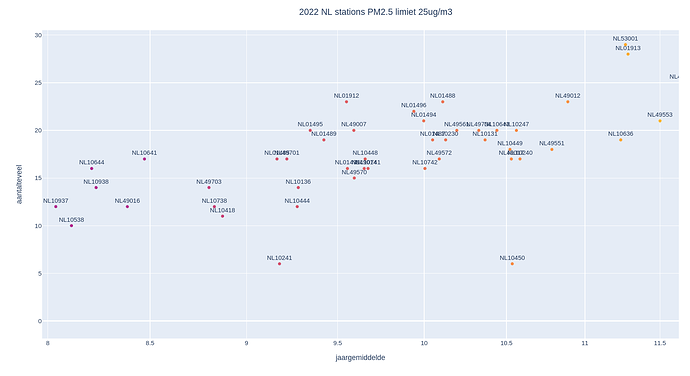
Wat Walters grafiek laat zien is een spreiding van x voor elke waarde van X. De kans van overschrijding met een aantal x0 is P(x>x0| M0). Elk jaar meten een 50 tal stations dit gemiddelde M0 - er zijn er met relatief hoge waardes (weinig) en relatief lage waardes (nog minder). Voor een drietal jaren geef ik hier een overzicht van jaargemiddeldes P25 voor alle officiële NL stations afgelezen uit LuchtMeetNet (in mijn software heten ze LM - Ik heb de naam NL gereserveerd voor stations die ik aflees van samenmeten.rivm.nl).
Ook hier vinden we dus een spreiding van waarden (tussen grofweg 8 en 15 mmgr/m3). Als we de totale kans voor een overschrijding willen berekenen moeten we de kansen P(x>x0|M0) integreren over de distributie van de mogelijke jaargemiddelde waarden.
De formulering is natuurlijk wat omslachtig, maar ook wel wat simplistisch. De aanname die impliciet wordt gemaakt is dat er een unieke distributie is voor x | M0 (aantal overschrijdingen voor een bepaald jaargemiddelde). Maar met deze simplistische methode is wel te rekenen. Als door beleidsmaatregelen de jaargemiddeldes naar beneden worden geschroefd, hebben we dus een nieuwe distributie voor de jaargemiddeldes en kunnen we met de eerder berekende kansverdelingen P(x>x0|M0) de totale kans op overschrijdingen berekenen.
Leuke wiskunde, en leuk om mee te spelen. Maar er is daarmee wel een aanname dat de kansverdelingen per jaar niet te veel zullen verschillen. We kunnen daar wel vraagtekens bij zetten.
De eerste vraag is - wat is de bron van de overschrijdingen?
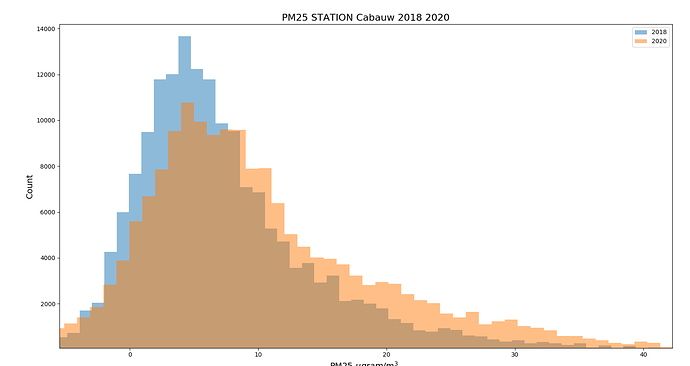
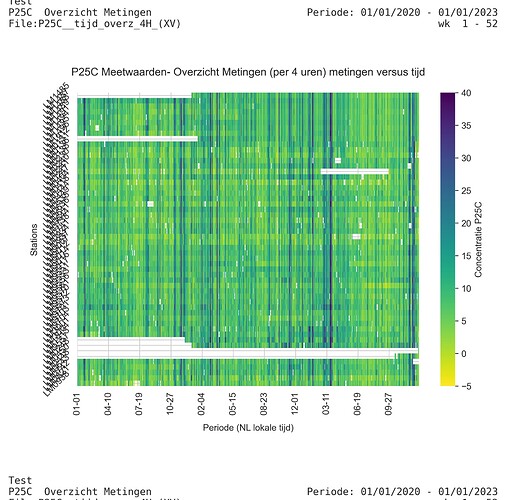
Als we naar de PM25 waarden kijken over de afgelopen 3 jaar (hier in een heatmap - tijd loopt van links naar rechts - elke rij representeert een LuchtMeetNet station), dan zien we dat extrema vaak bij alle stations min of meer tegelijk optreden. Dat kan twee dingen betekenen
1 - er gebeurt iets in heel Nederland dat de luchtkwaliteit aantast (vuurwerk, paasvuren, gaswolk uit raffinaderijen)
of
2. - het is een meteorologisch effect - modulatie door een dunne menglaag (hoge druk gebied met weinig wind), secundair fijnstof / ozon productie.
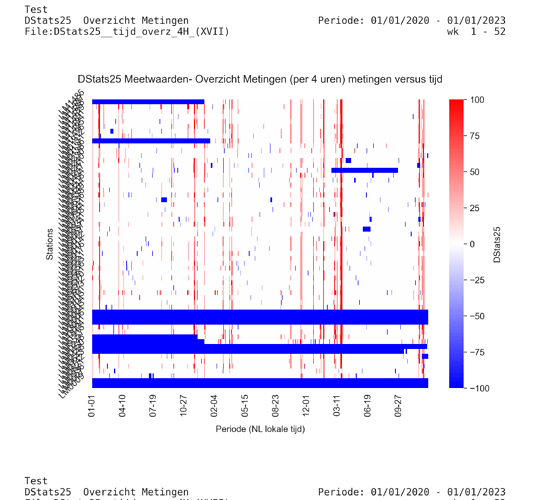
Maar er zijn ook meer geïsoleerde maxima. Als we kijken naar de dagoverschrijdingen van PM25 (met grens 25 mmg/m3) over de laatste drie jaar krijgen we het beeld hieronder. In rood zijn de overschrijdingen aangegeven, in blauw missende gegevens (door het LuchtMeetNet afgekeurde waardes) .
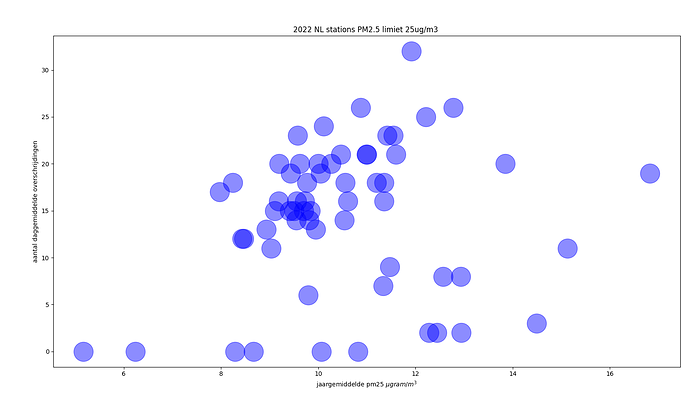
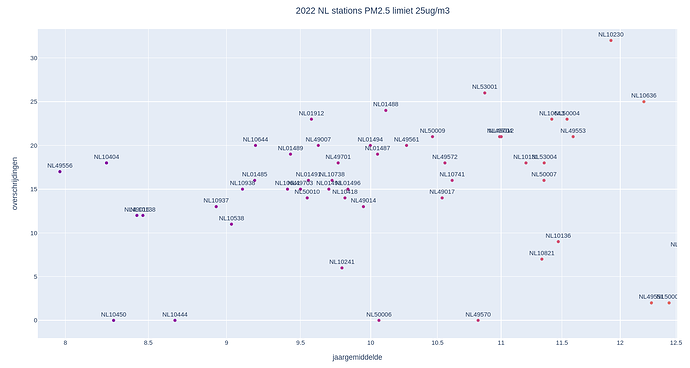
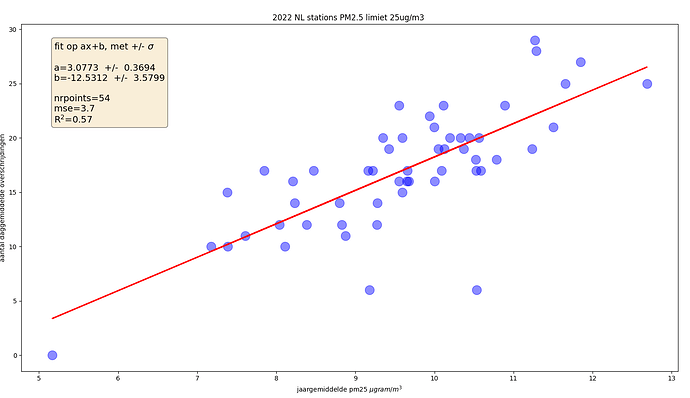
De vraag die blijft hangen is - wat zijn de bronnen en wat is het effect als de bron wordt aangepakt? Wat bepaalt de distributie van de punten op Walters grafiek? Als je van een afstandje kijkt lijkt het op een bipolaire distributie. Voor een aantal stations is het aantal overschrijdingen minder dan 10 mmgr/m3 ongeacht het jaargemiddelde, en voor de grootste groep is het aantal overschrijdingen ongeveer 18 mmgr/m3, met een schijnbare lineaire afhankelijkheid van het jaargemiddelde.
Vragen genoeg dus nog. En dan heb ik het nog niet eens over de vraag of de projecties voor jaargemiddeldes naar de toekomst reëel zijn. Houtstook is aanzienlijk en merkbaarder populairder geworden nu de prijs van gas hoog is. De stikstofplannen van het kabinet worden weer vertraagd - met gevolg voor de projecties voor secundair fijnstof .